Unit 4 introduces functions, focusing on notation, graphs, domain, range, and real-world applications. It provides structured lessons, video summaries, and practice problems to enhance understanding of function concepts.
1.1 Overview of Unit 4: Functions
Unit 4 focuses on functions, introducing notation, graphs, and key concepts like domain and range. Students explore piecewise and absolute value functions, inverse relationships, and real-world applications. The unit builds on middle school foundations, emphasizing problem-solving and graphical interpretation to deepen understanding of functional relationships and their practical uses in mathematics.
1.2 Importance of Functions in Algebra 1
Functions are foundational in Algebra 1, enabling students to model real-world relationships and solve problems. They help describe inputs and outputs, interpret graphs, and understand inverse relationships. Mastery of functions is crucial for advanced math, science, and problem-solving, making Unit 4 essential for building a strong mathematical foundation and analytical thinking skills.
Key Features of Functions in Unit 4
Unit 4 explores function notation, graphs, domain, range, piecewise functions, absolute value functions, and inverse functions, providing a comprehensive understanding of functions in Algebra 1.
2.1 Function Notation and Its Significance
Function notation, such as ( f(x) ), represents relationships between inputs and outputs. It allows precise communication of mathematical relationships, enabling the identification of specific output values for given inputs, like ( f(3) = 10 ), indicating the output when the input is 3. This notation is fundamental for analyzing and solving algebraic problems.
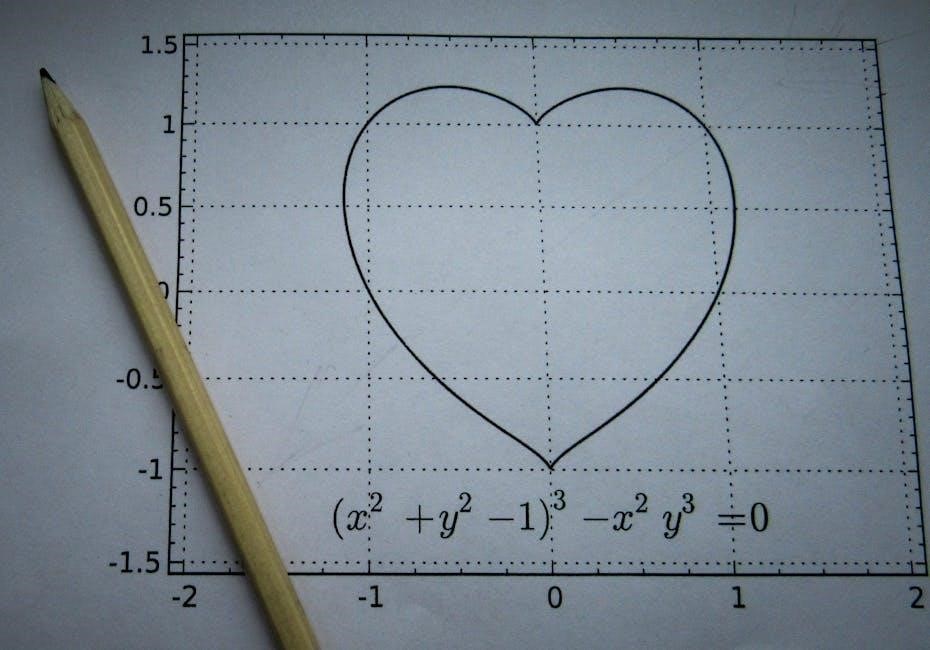
2.2 Graphs of Functions and Their Interpretation
Graphs of functions visually represent input-output relationships, allowing students to interpret key features such as increasing/decreasing intervals, maximum/minimum points, and intercepts. By analyzing graphs, students can estimate function values, understand domain and range, and connect graphical features to real-world contexts, enhancing their ability to sketch and interpret functions accurately.
2.3 Domain and Range of Functions
The domain of a function is the set of all possible input values, while the range is the set of all possible output values. Understanding domain and range is crucial for defining function behavior, identifying restrictions, and interpreting real-world applications. Students learn to determine these from function rules, graphs, or context, ensuring accurate function representation and analysis.
2.4 Piecewise and Absolute Value Functions
Piecewise functions involve different expressions for different input intervals, allowing complex behavior modeling. Absolute value functions, like ( f(x) = |x| ), create V-shaped graphs with a vertex and symmetry. Students learn to define, graph, and interpret these functions, understanding their real-world applications and how to translate verbal descriptions into mathematical expressions accurately.
2.5 Inverse Functions and Their Properties
Inverse functions reverse the mapping of original functions, satisfying ( f(f^{-1}(x)) = x ) and ( f^{-1}(f(x)) = x ). They are reflections over the line ( y = x ). To find an inverse, switch ( x ) and ( y ) in the original function and solve for ( y ). Inverse functions are essential for solving equations and modeling real-world relationships where reversal is necessary.

How to Find the Answer Key for Unit 4
Access the official Illustrative Mathematics Algebra 1 Unit 4 curriculum on their website or through authorized platforms. Supplementary resources like Khan Academy and Quizlet offer practice problems and answer keys for review.
3.1 Official Sources for the Answer Key
The official Illustrative Mathematics Algebra 1 Unit 4 answer key is available through their authorized curriculum platform. Access the complete curriculum materials, including lesson plans and assessments, directly from the Illustrative Mathematics website or through licensed partners like Kendall Hunt. The answer key is structured to align with specific lessons, providing detailed solutions and explanations for practice problems.
3.2 Supplementary Resources and Platforms
Beyond official sources, supplementary resources like Teachers Pay Teachers and YouTube offer answer key PDFs and video explanations. Platforms such as Khan Academy and Mathway provide additional support for complex problems. These resources complement the curriculum, offering alternative perspectives and practice materials to enhance understanding of Unit 4 concepts without replacing official materials.
Resources and Materials for Unit 4
Official Illustrative Mathematics resources include practice problems, video summaries, and answer keys. Additional materials, like worksheets and lesson plans, are available on educational platforms and teacher forums, supporting Unit 4 learning effectively.
4.1 Practice Problems and Worksheets
Illustrative Mathematics provides comprehensive practice problems and worksheets for Unit 4, focusing on functions, notation, and graph interpretation. These resources, including Unit 4 Lesson 1 and 2 Practice Problems, are supported by video explanations and supplementary materials, helping students master function concepts and apply them effectively in various mathematical contexts.
4.2 Video Explanations and Lesson Summaries
Video lesson summaries and explanations for Unit 4 are available, covering key concepts like function notation, graphs, domain, and inverse functions. These resources, aligned with Illustrative Mathematics’ curriculum, support student review and understanding through engaging explanations and structured overviews of each lesson’s main ideas and vocabulary.
Understanding the Structure of Functions in Unit 4
Unit 4 emphasizes representing functions algebraically and interpreting them graphically, connecting notation, graphs, and real-world applications to deepen understanding of function relationships and structures.
5.1 Representing Functions Algebraically
Algebraic representation of functions in Unit 4 involves using notation like ( f(t) ) for relationships such as distance over time. Students learn to express functions as equations, for instance, ( g(x) = 5x ) for cost per burrito. This connects algebraic forms to real-world contexts, enhancing understanding through practical examples and applications.
5.2 Interpreting Functions Graphically
Graphical interpretation involves analyzing function graphs to understand input-output relationships. Students learn to estimate values, identify key features like domain and range, and connect graphical characteristics to real-world contexts. This skill helps in sketching graphs from functions and interpreting their behavior, enhancing the ability to visualize and analyze functional relationships effectively.
5.3 Real-World Applications of Functions
Functions model real-world relationships, such as distance over time or cost versus quantity. Students explore practical examples, like the height of a plant or temperature changes, to understand how functions represent inputs and outputs in everyday contexts. This application helps connect abstract concepts to tangible scenarios, enhancing problem-solving skills and real-world relevance.
Common Challenges in Unit 4
Students often struggle with function notation interpretation, graph sketching, and understanding domain and range. These concepts require precise mathematical reasoning and visual representation skills, posing initial difficulties.
6.1 Understanding Function Notation
Function notation, like ( f(t) ), represents the output when ( t ) is the input. Challenges arise in interpreting notation, connecting it to graphs, and applying it to real-world scenarios. Students often struggle with distinguishing between function names and variables, leading to confusion in problem-solving. Practice with examples helps clarify these concepts and improves understanding.
6.2 Interpreting Key Features of Graphs
Interpreting key features of graphs involves identifying domain, range, intercepts, and intervals of increase or decrease. Challenges arise in connecting graphical features to real-world contexts and understanding their practical implications. Students often struggle with accurately identifying these elements, which are crucial for analyzing function behavior and solving problems effectively in Algebra 1 Unit 4.
6.3 Sketching Graphs from Functions
Sketching graphs from functions requires understanding function notation, domain, range, and key features like intercepts and intervals of increase or decrease. Challenges include accurately plotting points and translating function rules into visual representations. Practice with sample functions and review of answer keys can help students master this essential skill for analyzing function behavior.

Video Lesson Summaries for Unit 4
Video summaries cover key concepts across lessons, including functions, notation, graphs, domain, range, piecewise, absolute value, and inverse functions, aiding student review and understanding of complex topics.
7.1 Functions and Function Notation
Functions are relationships where inputs correspond to exactly one output. Function notation, like ( f(t) = 10 ) when ( t = 3 ), clearly represents these relationships. This notation simplifies communication and problem-solving in algebra, enabling students to interpret and manipulate functions effectively in various mathematical contexts and real-world applications.
7.2 Interpreting Function Notation
Function notation, such as ( f(t) = 10 ) when ( t = 3 ), allows students to interpret inputs and outputs clearly. This notation helps in understanding relationships, solving equations, and analyzing real-world problems. It enables precise communication of function behavior, making it easier to identify key features like domain, range, and transformations in algebraic expressions and graphical representations.

7.3 Graphs of Functions
Graphs of functions visually represent the relationship between inputs and outputs, allowing students to estimate values and understand function behavior. By analyzing graphs, students can identify key features such as increasing/decreasing intervals, maximum/minimum points, and intercepts. This visual tool helps connect algebraic representations to real-world applications, enhancing comprehension of how functions model various scenarios and relationships.
7.4 Making and Interpreting Graphs
Making and interpreting graphs helps students visualize function behavior, identify key features, and connect algebraic representations to real-world contexts; By sketching graphs, students develop skills in identifying intercepts, intervals of increase/decrease, and maxima/minima. This process enhances their ability to interpret and communicate mathematical relationships effectively, supporting problem-solving in various scenarios.
7.5 Domain and Range
Domain and range are essential concepts in function analysis. The domain refers to all possible input values (x-values), while the range consists of all possible output values (y-values); Students learn to identify these from function definitions, graphs, or tables. Understanding domain and range is critical for interpreting function behavior and solving real-world problems effectively.
7.6 Piecewise and Absolute Value Functions
Piecewise functions involve multiple expressions over different intervals, while absolute value functions represent distance from zero. Students analyze these using function notation and graphs, identifying key features like corners, cusps, and V-shapes. These concepts are crucial for modeling real-world scenarios, such as ticket prices or distance problems, enhancing problem-solving skills.
7.7 Inverse Functions
Inverse functions reverse the action of another function, denoted by f⁻¹(x). To find an inverse, swap x and y, then solve for y. The graph of an inverse function is the reflection of the original function’s graph over the line y = x. Inverse functions are essential for solving equations and understanding one-to-one relationships.
The Answer Key Structure
The answer key is organized by lesson, providing step-by-step solutions for practice problems, ensuring clarity and ease of understanding for students reviewing their work.
8.1 Format and Organization
The answer key is structured by lesson and standard, offering clear solutions to practice problems. It includes step-by-step explanations, aligning with the curriculum’s focus on functions, graphs, and real-world applications. The format ensures ease of navigation, with problems numbered and solutions concise, adhering to Illustrative Mathematics’ standards for clarity and educational support.
8.2 Types of Problems Included
The answer key includes a variety of problems such as function notation, graph interpretation, domain and range identification, and solving piecewise and absolute value functions. It also covers inverse functions and real-world applications, ensuring comprehensive coverage of key concepts in Unit 4.
8.3 Solutions and Explanations
The answer key provides detailed solutions and explanations for various problems, including step-by-step breakdowns of function notation, graph interpretations, and inverse functions. It clarifies common misunderstandings and offers insights into problem-solving strategies, ensuring students grasp key concepts effectively.
Tips for Using the Answer Key Effectively
Use the answer key for self-assessment, review mistakes, and understand problem-solving strategies. Focus on understanding concepts rather than just answers, and supplement with video explanations for deeper insights.
9.1 Best Practices for Reviewing Solutions
Review solutions systematically by comparing your work step-by-step. Understand the reasoning behind each answer to grasp concepts deeply. Highlight and note areas of difficulty, then revisit challenging problems after initial review for better retention and understanding of function principles.
9.2 Avoiding Common Mistakes
Common mistakes include misinterpreting function notation and incorrectly identifying domain and range. To avoid these, carefully analyze each step, ensure understanding of function definitions, and double-check interpretations of graphs and tables. Regular practice and reviewing solutions can help identify and correct these errors effectively.

Availability of the Answer Key
The official answer key is available through authorized sources, while third-party platforms offer supplementary materials. Ensure materials are from trusted providers to maintain quality and compliance.
10.1 Official Availability
The official answer key for Illustrative Mathematics Algebra 1 Unit 4 is available through authorized sources, including the Illustrative Mathematics website and licensed partners. Access requires approval, ensuring materials are used under the Creative Commons Attribution 4.0 license. The PDF format is provided for convenience, allowing teachers and students to review solutions effectively while adhering to copyright guidelines.
10.2 Third-Party Resources
Third-party platforms like Teachers Pay Teachers (TPT) and educational websites offer supplementary answer keys and resources for Algebra 1 Unit 4. These materials, while not officially endorsed, provide additional practice problems, video explanations, and lesson summaries. They are useful for reinforcing concepts but should be verified for accuracy and alignment with official content.
Unit 4 provides foundational knowledge of functions, essential for algebraic understanding. Utilizing official and third-party resources ensures comprehensive learning and mastery of key concepts effectively.
11.1 Summary of Key Takeaways
Unit 4 focuses on functions, covering notation, interpretation, graphs, domain, range, piecewise functions, and inverses. It emphasizes real-world applications and provides resources like video lessons and practice problems to reinforce understanding and mastery of function concepts effectively.
11.2 Final Thoughts on Mastering Unit 4
Mastering Unit 4 requires consistent practice and a deep understanding of function concepts. Focus on interpreting notation, analyzing graphs, and applying functions to real-world scenarios. Utilize available resources, such as video lessons and practice problems, to reinforce learning. Regularly reviewing answer keys and explanations will help solidify understanding and improve problem-solving skills effectively.
Final Note on Illustrative Mathematics Resources
Illustrative Mathematics provides comprehensive resources under a Creative Commons license, ensuring accessible and high-quality materials for learning and teaching Algebra 1, Unit 4.
12.1 Creative Commons License and Usage
Illustrative Mathematics resources, including Algebra 1 Unit 4, are licensed under Creative Commons Attribution 4.0. This allows free use, sharing, and adaptation with proper attribution. The IM name and logo, however, are not covered by this license and require explicit permission for use. Users must respect these terms to ensure legal and ethical usage of the materials.
12.2 Importance of Authorized Materials
Using authorized Illustrative Mathematics materials ensures compliance with licensing terms and maintains content quality. It supports the integrity of the curriculum and protects the intellectual property of the organization. Students and educators benefit from accurate, reliable resources, fostering effective learning and teaching experiences while adhering to legal and ethical standards.